点集拓扑 4 - 连续函数与同胚

2024-03-28

本文内容已完全施工完毕, 读者可放心阅读！

本文最后更新日期：2024-04-09

4.1. 连续函数

定义 4.1.1 (连续函数)

设 $(X, \tau_X)$ 与 $(Y, \tau_Y)$ 为拓扑空间, 若称 $f : (X, \tau_X) \to (Y, \tau_Y)$ 为 连续函数 / 连续映射 (continuous function / continuous map), 当 $f$ 中 $Y$ 的任意开集的原像仍是 $X$ 中的开集, 具体即为： $$
\text{$f$ 连续} \coloneqq \Forall{O \in \tau_Y} f^{-1}(O) \in \tau_X

$$

命题 4.1.2 (连续函数于闭集下的等价定义)

设 $(X, \tau_X)$ 与 $(Y, \tau_Y)$ 为拓扑空间, 若 $f : (X, \tau_X) \to (Y, \tau_Y)$ 是连续的当且仅当 $f$ 中 $Y$ 的任意闭集的原像仍是 $X$ 中的闭集.

注释 (全体拓扑空间构成具体范畴)

若将拓扑空间视为范畴中的对象, 并且以连续函数作为当中的态射, 则可验证其的确构成拓扑空间范畴, 记为 $\Top$;
若假设有集合范畴 $\Sets$, 且定义 $\Map{U}{\Top}{\Sets}{(X, \tau_X)}{X}$ 为 遗忘函子 (forgetful functor), 意味着 $U$ 是 忠实 (faithful) 的, 即下述映射是单射的： $$
\map{\op{Top}((X, \tau_X), (Y, \tau_Y))}{\Sets(U((X, \tau_X)), U((Y, \tau_Y)))}{\bb{(X, \tau_X) \overset{\text{连续函数}}{\to} (Y, \tau_Y)}}{\bb{X \overset{\text{函数}}{\to} Y}}

$$
若任意范畴携带了从其到集合范畴的忠实函子, 则该范畴被称为 具体范畴 (concrete category), 显然 $\Top$ 便是具体范畴.

例子 4.1.3 (乘积拓扑空间的函子性)

考虑以下连续函数： $$
f_1 : (X_1, \tau_{X_1}) \to (Y_1, \tau_{Y_1}) \qquad f_2 : (X_2, \tau_{X_2}) \to (Y_2, \tau_{Y_2})

$$ 则可诱导出它们在基础集的二元积上的函数 $\Map{f_1 \times f_2}{X_1 \times X_2}{Y_1 \times Y_2}{(x_1, x_2)}{(f_1(x_1), f_2(x_2))}$, 且 $f_1 \times f_2$ 亦表示了是从二元乘积拓扑空间 $X_1 \times X_2$ 到 $Y_1 \times Y_2$ 的连续函数, 即： $$
(X_1 \times X_2, \tau_{X_1 \times X_2}) \overset{f_1 \times f_2}{\to} (Y_1 \times Y_2, \tau_{Y_1 \times Y_2})

$$ 易见乘积拓扑空间这一构成过程是函子式的, 因为可引出以下从拓扑空间的乘积范畴 $\Top \times \Top$ 到 $\Top$ 的函子 $(-) \times (-)$： $$
\Map{(-) \times (-)}{\Top \times \Top}{\Top}{((X_1, \tau_{X_1}), (X_2, \tau_{X_2}))}{(X_1 \times X_2, \tau_{X_1 \times X_2})}

$$

其中 $\tau_{X_1 \times X_2}$ 为由原先分别于 $X_1, X_2$ 中的拓扑基 $U_1 \in \tau_{X_1}$ 以及 $U_2 \in \tau_{X_2}$ 的笛卡尔积 $U_1 \times U_2$ 所生成的拓扑.

例子 4.1.4 ($\Top$ 中的始对象与终对象)

设 $(X, \tau)$ 为拓扑空间, 则必然存在唯一的连续函数：

从空拓扑空间到 $X$ 的连续函数 $\empty \overto{\exists!} X$, 其中 $\empty$ 为 $\Top$ 中的始对象;
从 $X$ 到点拓扑空间的连续函数 $X \overto{\exists!} *$, 其中 $*$ 为 $\Top$ 中的终对象.

例子 4.1.5 (常连续函数)

设 $(X, \tau)$ 为拓扑空间以及任取一点 $x \in X$, 则存在唯一的连续函数 $* \overset{x}{\to} X$ 使得该映射的像恰好便是点 $x$, 因此事实上对于任意点 $x \in X$ 则可得出以下这个双射关系： $$
\Set{ * \overset{f}{\to} X : \text{$f$ 是连续的} } \simeq X

$$

更进一步地, 对于任意拓扑空间 $(X, \tau_X)$ 以及 $(Y, \tau_Y)$, 若连接它们之间的连续函数 $f : (X, \tau_X) \to (Y, \tau_Y)$ 被称为映射至某一点 $y \in Y$ 的常函数, 则存在映射分解 $c_y : X \overset{\exists!}{\to} * \overset{y}{\to} Y$.

定义 4.1.6 (局部常函数)

设 $(X, \tau_X), (Y, \tau_Y)$ 均为拓扑空间, 以及连续函数 $f : (X, \tau_X) \to (Y, \tau_Y)$, 若对于任意点 $x \in X$ 都存在它的邻域 $U \sub X$ 使得 $f$ 在 $U$ 中是常函数, 即对于任意 $u, v \in U$, 有 $f(u) = f(v)$, 则称 $f$ 为 局部常函数 (locally constant function).

例子 4.1.7 (连续函数与离散/余离散拓扑空间)

设有任意集合 $S$ 以及 $(X, \tau)$ 为拓扑空间, 则：

任意从离散拓扑空间到 $X$ 的函数 $\Disc{S} \to X$ 都是连续的;
任意从余离散拓扑空间到 $X$ 的函数 $X \to \CoDisc{S}$ 都是连续的;
任意从 $X$ 到离散拓扑空间的连续函数 $X \to \Disc{S}$ 是局部常函数.

证明

由于对任意 $X$ 中的开集 $O \in \tau_X$, 其的原像 $f^{-1}(O) \in \mathcal{P}(S) = \tau_{\Disc{S}}$, 显然 $\Disc{S} \to X$ 是连续的.
由于任意开集 $O \in \CoDisc{S} = \set{\empty, S}$, 那么分类讨论：
- 当 $f^{-1}(\empty)$, 根据空集的原像为空, 则推得 $f^{-1}(\empty) = \empty \in \tau_X$;
- 当 $f^{-1}(S)$, 显然其原像便是 $X \in \tau_X$.
因此函数 $X \to \CoDisc{S}$ 是连续的.
由于 $\Disc{S}$ 是离散的当且仅当其的独点集 $\set{y}$ 是 $\Disc{S}$ 中的开集, 若 $f : X \to \Disc{S}$ 为连续函数, 则推得 $f^{-1}(\set{y})$ 为 $X$ 中的开集, 现在假设有常函数 $f(x) = y$, 那么 $x \in f^{-1}(\set{y})$ 且 $f^{-1}(\set{y})$ 是开的, 因此对于任意点 $x \in X$, 都存在开邻域 $f^{-1}(\set{y})$ 使得满足了 $f(x) = y$, 所以 $f$ 为局部常函数.

例子 4.1.8 (对角)

设 $X$ 为任意集合, 映射 $\Map{\Delta_X}{X}{X \times X}{x}{(x, x)}$ 被称为 $X$ 的 对角 (diagonal), 记为 $\Delta_X$.
特别地若 $(X, \tau)$ 为拓扑空间, 则其的对角化构成连续函数 $(X, \tau) \to (X \times X, \tau_{X \times X})$, 因为对于 $\tau_{X \times X}$ 中的拓扑基 $U_1 \times U_2$, 根据拓扑公理, 其原像 $U_1 \cap U_2$ 仍是 $X$ 中的开集.

例子 4.1.9 (连续函数的像分解)

设 $f : (X, \tau_X) \to (Y, \tau_Y)$ 为连续函数, 则可将 $f$ 分解为以下连续函数的复合形式： $$
f : X \overset{\text{满射}}{\to} f(X) \overset{单射}{\to} Y

$$ 这意味着我们需要 "拓扑化" $f(X)$, 因此我们有以下两种方式将其化为拓扑空间：

从子空间拓扑的角度考虑, 由于 $f(X)$ 可作为 $Y$ 的子空间, 即是说 $f(X)$ 与子空间拓扑 $\tau_{f(X)} = \tau_Y \cap f(X)$ 组成了拓扑空间, 显然由于 $f(X) \sub Y$ 就使得存在 $f(X) \to Y$ 的单射连续函数. 另一方面, 由于 $X \to f(X)$ 显然为满射, 且对于任意 $O \in \tau_{f(X)}$, 则可使得 $f^{-1}(O) \in \tau_X$, 这是因为 $\tau_{f(X)} = \tau_Y \cap f(X)$ 蕴含了 $O \in \tau_Y$, 当 $f$ 为连续函数时 $O$ 于 $X$ 中是开的, 因此 $X \to f(X)$ 为连续函数.
从商空间拓扑的角度考虑, 由于可将 $f(X)$ 视为是 $X$ 的商拓扑空间, 那么满射 $\pi : X \to f(X)$ 便是典范投射. 另一方面, 对于任意 $O \in \tau_Y$, 有 $f^{-1}(O) \in \tau_Y \cap f(X)$, 而对于任意 $U \in \tau_Y \cap f(X)$, 由于 $f$ 为连续函数, 则有 $f^{-1}(U) \in \tau_X$, 因此 $U$ 于商拓扑空间 $f(X)$ 中亦是开的.

注释

然而更广义地, 连续函数本身并不会保有拓扑空间中的开集亦或是闭集, 例如以下这些例子.

例子 4.1.10 (连续函数不保有开/闭集的例子)

下述均假设 $\R$ 为携带了度量拓扑的欧氏空间：

若有 $a \in \R$ 使得 $\R$ 中有连续的常值函数 $\Map{c_a}{\R}{\R}{x}{a}$, 即对于任意 $x \in \R$ 都要映射至 $a$ 中, 意味着任意开集都被映射至闭的独点集 $\set{a}$ 中.
假设有从 $\R$ 的离散拓扑到 $\R$ 的恒同连续函数 $\text{id}_{\R} : \Disc{\R} \to \R$, 显然独点集 $\set{a} \in \Disc{\R}$ 是开的却于 $\R$ 中是闭的.
指数函数 $\exp(-) : \R \to \R$ 将所有 $\R$ 中的元素 ($\R = \R \backslash \empty$, 因此 $\R$ 是闭集) 映射至开区间 $(0, \infin) \sub \R$ 中.

因此上述这些连续函数皆不保有开/闭集关系.

定义 4.1.11 (开映射与闭映射)

设有连续函数 $f : (X, \tau_X) \to (Y, \tau_Y)$：

若 $\Forall{O \in \tau_X} f(O) \in \tau_Y$, 则 $f$ 被称为 开映射 (open map);
若 $\Forall{\text{$C$ 为闭集}} \text{$f(C)$ 为闭集}$, 则 $f$ 被称为 闭映射 (closed map).

例子 4.1.12 (开/闭映射的像投射本身亦是开/闭的)

若连续函数 $f : (X, \tau_X) \to (Y, \tau_Y)$ 是开/闭映射, 则其像的投射 $X \to f(X) \sub Y$ 仍是开/闭映射的, 其中 $f(X)$ 为子空间.

证明

假设 $f(X)$ 的拓扑为 $\tau_{f(X)} \coloneqq \tau_Y \cap f(X)$, 由于 $f$ 本身为开映射, 因此对于任意 $O \in \tau_X$ 有 $f(O) \in \tau_Y$, 并且 $f(O) \sub f(X)$ 便使得 $f(O) \sub \tau_Y \cap f(X) = \tau_{f(X)}$, 因此其于 $f(X)$ 中仍为开集, 对于闭映射的证明方式亦然.

例子 4.1.13 (投射为开连续函数)

设 $(X_1, \tau_{X_1})$ 与 $(X_2, \tau_{X_2})$ 为拓扑空间, 则由它们所组成的乘积拓扑空间的 (连续) 投射是开映射 (其中 $i = 1, 2$)： $$
\Map{\op{pr}_i}{(X_1 \times X_2, \tau_{X_1 \times X_2})}{(X_i, \tau_{X_i})}{(x_1, x_2)}{x_i}

$$ 这是因为拓扑 $\tau_{X_1 \times X_2}$ 中的任意开集 $O \sub X_1 \times X_2$ 完全由基 $\mathcal{B} \sub \tau_{X_1 \times X_2}$ 所生成, 即 $\ds \Set{ \bigcup_{U_1 \times U_2 \in \beta} (U_1 \times U_2) : U_1 \in \tau_{X_1}, U_2 \in \tau_{X_2} }$, 显然： $$
\op{pr}_i \b{\bigcup_{U_1 \times U_2 \in \beta} (U_1 \times U_2)} \overset{\text{函数的像保有并}}{=} \bigcup_{U_1 \times U_2 \in \beta} \op{pr}_i (U_1 \times U_2) = \bigcup_{i \in I} U_i \in \tau_{X_i}

$$

定义 4.1.14 (饱和集)

对于任意函数 $f : X \to Y$, 若子集 $S \sub X$ 被称为 $f$-饱和集 ($f$-saturated set), 当 $S$ 的像的原像等价于它自身, 即： $$
\text{$S \sub X$ 为 $f$ 的饱和集} \iff S = f^{-1}(f(S))

$$ 其中 $f^{-1}(f(S))$ 亦被称为 $S$ 的 $f$-饱和化 ($f$-saturation).

例子 4.1.15 (原像为饱和集)

对于任意函数 $f : X \to Y$, 以及任意子集 $S \sub Y$, 则原像 $f^{-1}(S) \sub X$ 为 $f$-饱和集

证明

$$
f^{-1}(f(f^{-1}(S))) = \set{ x \in X : f(x) \in f(f^{-1}(S)) } = \set{ x \in X : x \in f^{-1}(S) } = f^{-1}(S)

$$

引理 4.1.16 (饱和集的等价定义)

对于任意函数 $f : X \to Y$, 若子集 $S \sub X$ 为 $f$-饱和集 $\iff$ 其补集 $X \backslash S$ 也是饱和的.

证明

$$
\begin{align}
X \backslash S & = X \backslash f^{-1}(f(S)) \\
& = \set{ x \in X : x \notin f^{-1}(f(S)) } \\
& = \set{ x \in X : f(x) \notin f(S) } \\
& = \set{ x \in X : f(x) \in f(X \backslash S) } \\
& = f^{-1}(f(X \backslash S)) \\
\end{align}

$$

命题 4.1.17 (商拓扑空间的等价定义)

设 $f : (X, \tau_X) \to (Y, \tau_Y)$ 为连续函数, 则以下命题等价：

若底层函数 $f : X \to Y$ 为满射且 $\tau_Y$ 为商拓扑 (该条件等价于说 $f$ 为商映射).
$f$ 将 $X$ 中的开 $f$-饱和集映射至 $Y$ 中的开集.
$f$ 将 $X$ 中的闭 $f$-饱和集映射至 $Y$ 中的闭集.

证明

只证明 $(1) \lrArr (2)$, 因为 $(3)$ 由引理 4.1.16 给出. 下设 $S$ 为 $X$ 中的开 $f$-饱和集：

$(\rArr)$ 设 $f$ 为满射且满足 $\tau_Y = \set{ O \sub Y : f^{-1}(O) \in \tau_X }$, 需要验证 $f(S) \in \tau_Y$, 那么按 $\tau_Y$ 的定义： $$
f^{-1}(f(S)) \overset{\text{$S$ 饱和}}{=} S \overset{\text{$S$ 开}}{\in} \tau_X

$$ $(\lArr)$ 反之若设 $\Forall{\text{开饱和集 $S \sub \tau_X$}} f(S) \in \tau_Y$, 且令 $Y = X/\sim$, 需要分别验证商映射的条件：

$f$ 为满射, 这是显然的.
$f$ 为商映射, 即需验证 $\Forall{U \sub Y} U \in \tau_{Y} \iff f^{-1}(U) \in \tau_X$, 分别讨论：

$(\rArr)$ $\Forall{\text{开集 $U \in \tau_Y$}} f^{-1}(U) \in \tau_X$, 这由 $f$ 是连续函数直接给出.

$(\lArr)$ 由于 $f^{-1}(U) \in \tau_X$ 是开的, 由例子 4.1.15 易知 $f^{-1}(U)$ 亦饱和, 因此由假设得 $f(f^{-1}(U)) \in \tau_Y$.

引理 4.1.18 (于闭映射下的饱和闭集的饱和开邻域)

设有以下条件：

$f : (X, \tau_X) \to (Y, \tau_Y)$ 为闭映射;
$C \sub X$ 为 $X$ 的闭集且其是 $f$-饱和的;
$U \supset C$ 为包含了 $C$ 的开集;

则存在最小的开 $f$-饱和集 $V$ 仍包含了 $C$, 即 $U \supset V \supset C$.

4.2. 同胚

定义 4.2.1 (同胚映射)

设 $X, Y$ 为拓扑空间, 若 $f : X \to Y$ 是一个双射, 并且 $f$ 与 $f^{-1}$ 都是连续的, 则：

称 $f$ 为一个 同胚映射 / 同胚 / 拓扑同构 (homeomorphism / topological isomorphism).
称拓扑空间 $X$ 与 $Y$ 是 同胚的 (homeomorphic), 或称 $X$ 同胚于 $Y$.

注释

若 $f$ 为同胚, 则 $f$ 的逆连续函数 $g = f^{-1}$ 仍是同胚;
给定任意关于拓扑空间的命题/性质 $P$, 总是有以下的不变量： $$
\bigg( (X_, \tau_X) \simeq (Y, \tau_Y) \bigg) \implies \bigg( P(X_, \tau_X) \iff P(Y, \tau_Y) \bigg)

$$ 这被称为 $(X_, \tau_X)$ 与 $(Y, \tau_Y)$ 之间的 同胚不变量 (homeomorphism invariants).
事实上拓扑空间范畴 $\Top$ 中的同构关系便是同胚, 因此将保有以下的基本性质.

命题 4.2.2 (同胚映射的基本性质)

设 $X, Y, Z$ 为拓扑空间, 则：

恒同映射 $1_X : X \to X$ 同胚;
若有同胚 $f : X \to Y$, 则 $f^{-1} : Y \to X$ 亦同胚;
若有同胚 $f : X \to Y$ 以及 $g : Y \to Z$, 则 $g \circ f : X \to Z$ 同胚.

注释

需要注意的是, 并非任意双射的连续函数都是同胚的, 因为其的逆函数可能并不连续, 例如以下这个反例.

例子 4.2.3 ($[0, 2\pi)$ 与 $S^1$)

考虑从半开区间 $[0, 2\pi)$ 到单位圆 $S^1$ (即作为 $2$ 维欧氏空间 $\R^2$ 的子空间) 的连续映射 $\map{[0, 2\pi)}{S^1 \sub \R^2}{t}{(\cos(t), \sin(t))}$, 其虽然是个双射, 但它的逆函数于点 $(1, 0) \in S^1 \sub \R^2$ 却并非连续, 因此 $f$ 并不是同胚.
另一方面, 我们可以由一些 拓扑不变量 (topological invariants) 判断两个空间之间是否同胚, 例如接下来将会提及到 $S^1$ 本身是紧拓扑空间而 $[0, 2\pi)$ 并非, 那么 $S^1$ 有非平凡的 基本群 (fundamental group) 而 $[0, 2\pi)$ 为平凡的, 因此两者不可能同胚.

命题 4.2.4 (同胚是连续的开双射)

设 $f : (X, \tau_X) \to (Y, \tau_Y)$ 为连续函数, 则以下条件是等价的：

$f$ 为同胚;
$f$ 为双射且为开映射;
$f$ 为双射且为闭映射.

例子 4.2.5 (独点集同胚于点拓扑空间)

设 $(X, \tau_X)$ 为非空拓扑空间, 以及任意点 $x \in X$, 则独点集 $\set{x} \sub X$ 携带它的子空间拓扑 $\tau_{\set{x}}$ 所构成的空间同胚于点拓扑空间, 即： $$
(\set{x}, \tau_{\set{x}}) \simeq *

$$

例子 4.2.6 (开区间同胚于实数轴)

设 $\R$ 为携带了度量拓扑的欧氏空间, 则开区间 $(-1, 1) \sub \R$ 以及其的子空间拓扑所构成的子空间同胚于 $\R$, 即 $(-1, 1) \simeq \R$, 因为我们可以给出一对互逆的连续映射, 例如： $$
\lrmap{\R}{(-1, 1)}{x}{\frac{x}{\sqrt{1 + x^2}}}{\frac{x}{\sqrt{1 - x^2}}}{x}

$$

上述这一对连续映射不一定唯一, 我们还有很多其他取法使得它构成同胚. 类似地, 对任意 $a < b \in \R$ 还有以下结论：

任意开区间 $(a, b) \sub \R$ 连带它的子空间拓扑, 它们之间是相互同胚的.
任意半开区间 $[a, b)$ 之间是相互同胚的.
任意半开区间 $(a, b]$ 之间是相互同胚的.

更广义的说, 对任意 $\R^n$ 中的开球 $B^\circ_0(\epsilon)$ 连带它的子空间拓扑, 皆有同胚 $B^\circ_0(\epsilon) \simeq \R^n$.

例子 4.2.7 (广义乘积空间之间的同胚)

由 [例子 4.1.3](#例子 4.1.3 (乘积拓扑空间的函子性)) 我们知道乘积拓扑空间可被视为函子 $(-) \times (-) : \Top \times \Top \to \Top$, 而 $\Top$ 连带该函子天然地构成了对称幺半范畴. 具体的说, 考虑任意拓扑空间 $W, X, Y, Z \in \Top$ 及以下四个同胚：

结合子 (associator)：$\alpha_{X, Y, Z} : (X \times Y) \times Z \overto{\simeq} X \times (Y \times Z)$;
左单位子 (left unitor)：$\lambda_X : * \times X \overto{\simeq} X$;
右单位子 (right unitor)：$\rho_X : X \times * \overto{\simeq} X$;
辩 (braiding)：$\beta_{X, Y} : X \times Y \overto{\simeq} Y \times X$.

使得以下一系列图表可交换, 以及保证了对称性：

三角恒等式 (triangle identity)： $$

\xymatrix{
(X \times *) \times Y \ar@{->}[rd]_{\rho_X \times 1_Y} \ar@{->}[rr]^{{\alpha_{X, *, Y}}} & & X \times (* \times Y) \ar@{->}[ld]^{1_X \times \lambda_Y} \\
& X \times Y &
}

$$
五角形恒等式 (pentagon identity)： $$

\xymatrix{
& & ((W \times X) \times Y) \times Z \ar@{->}[lld]_{{\alpha_{W, X, Y} \times 1_Z}} \ar@{->}[rrd]^{{\alpha_{W \times X, Y, Z}}} & & \\
(W \times (X \times Y)) \times Z \ar@{->}[rd]_{{\alpha_{W, X \times Y, Z}}} & & & & (W \times X) \times (Y \times Z) \ar@{->}[ld]^{{\alpha_{W, X, Y \times Z}}} \\
& W \times ((X \times Y) \times Z) \ar@{->}[rr]_{{1_W \times \alpha_{X, Y, Z}}} & & W \times (X \times (Y \times Z)) &
}

$$
六角形恒等式 (hexagon identities)： $$

\xymatrix{
(X \times Y) \times Z \ar@{->}[r]^{{\alpha_{X, Y, Z}}} \ar@{->}[d]_{{\beta_{X, Y} \times 1_Z}} & X \times (Y \times Z) \ar@{->}[r]^{{\beta_{X, Y \times Z}}} & (Y \times Z) \times X \ar@{->}[d]^{{\alpha_{Y, Z, X}}} & & X \times (Y \times Z) \ar@{->}[d]_{{1_X \times \beta_{Y, Z}}} \ar@{->}[r]^{{(\alpha_{X, Y, Z})^{-1}}} & (X \times Y) \times Z \ar@{->}[r]^{{\beta_{X \times Y, Z}}} & Z \times (X \times Y) \ar@{->}[d]^{{(\alpha_{Z, X, Y})^{-1}}} \\
(Y \times X) \times Z \ar@{->}[r]_{{\alpha_{Y, X, Z}}} & Y \times (X \times Z) \ar@{->}[r]_{{1_Y \times \beta_{X, Y}}} & Y \times (Z \times X) & & X \times (Z \times Y) \ar@{->}[r]_{{(\alpha_{X, Z, Y})^{-1}}} & (X \times Z) \times Y \ar@{->}[r]_{{\beta_{X, Z} \times 1_Y}} & (Z \times X) \times Y
}

$$
对称性 (symmetry)： $$
\beta_{Y, X} \circ \beta_{X, Y} = \id : X \times Y \to X \times Y

$$

而由范畴论中其中一个著名的结论, 称之为 MacLane 融贯定理 (MacLane coherence theorem), 它保证了我们无论怎样挪动其中的括号, 使得结合顺序发生改变, 皆不会影响最终乘积空间之间是同胚的.

例子 4.2.8 (区间的乘积同胚于超立方体)

令 $n \in \N$, 分别考虑：

一族闭区间 $\Set{ [a_i, b_i] \sub \R }_{1 \leq i \leq n}$ (其中 $a_i \leq b_i$), 它们连同由 $\R$ 所诱导出的度量拓扑 $\tau_i \sub \mathcal{P}(\R)$ 组成了拓扑空间 $([a_i, b_i], \tau_i)$;
而上述闭区间 $[a_i, b_i]$ 的笛卡尔积连同乘积拓扑 $\tau_\text{Prod}$ 构成了乘积空间 $\ds \b{\prod_{1 \leq i \leq n} [a_i, b_i], \tau_\text{Prod}}$;
子集 $\ds S_\leq \colon \Set{ \vec{x} \in \R^n : \Forall{1 \leq i \leq n} a_i \leq x_i \leq b_i } \sub \R^n$ 连同 $\R^n$ 中的子拓扑 $\tau_\text{Sub}$ 同样构成子空间 $\ds \b{S_\leq, \tau_\text{Sub}}$.

则可得到以下同胚： $$
\b{\prod_{1 \leq i \leq n} [a_i, b_i], \tau_\text{Prod}} \simeq \b{S_\leq, \tau_\text{Sub}}

$$ 开区间也是类似的, 换言之我们有： $$
\b{\prod_{1 \leq i \leq n} (a_i, b_i), \tau_\text{Prod}} \simeq \b{S_<, \tau_\text{Sub}}

$$

证明

只证闭区间的情形, 开区间是类似的. 考虑映射 $\ds \varphi : \b{\prod_{1 \leq i \leq n} [a_i, b_i], \tau_\text{Prod}} \to \b{S_\leq, \tau_\text{Sub}}$ 显然在基础集上保持了双射, 而 $\tau_\text{Prod}$ 的基被取为： $$
\mathcal{B} \coloneqq \Set{ \prod_{1 \leq i \leq n} (a_i, b_i) \sub \R^n : (a_i, b_i) \in \tau_i }

$$ 由先前的拓扑基测试, 我们可以证明 $\mathcal{B}$ 也是 $\tau_\text{Sub}$ 的基：

$\mathcal{B}$ 覆盖了 $S_{\leq}$：对任意 $\vec{x} \in S_{\leq}$, 总能够找到 $\mathcal{B}$ 中一个开区间之积使得 $\vec{x} \in \ds \prod_{1 \leq i \leq n} (x_i - 1, x_i + 1)$.
对任意 $\mathcal{B}$ 中的 $B_1 = \ds \prod_{1 \leq i \leq n} (a_i, b_i)$ 以及 $B_2 = \ds \prod_{1 \leq i \leq n} (c_i, d_i)$, 显然对任意 $\ds \vec{x} \in B_1 \cap B_2$ 总是有 $\ds \vec{x} \in \prod_{1 \leq i \leq n} \big(\max(a_i, c_i), \min(b_i, d_i)\big) \sub B_1 \cap B_2$ 成立.

因此由 $\mathcal{B}$ 所生成的拓扑 $\tau_\text{Prod} = \tau_\mathcal{B}$ 必定等价于 $\tau_\text{Sub}$, 显然 $\tau_\text{Prod}$ 与 $\tau_\text{Sub}$ 中的开集于双射 $\varphi$ 下互相为对方的开集, 因此 $\varphi$ 是连续的.

例子 4.2.9 (闭区间于端点处粘合同胚于单位圆)

考虑空间 $\R$ 中的闭区间 $[0, 1]$, 如果我们将该区间两侧端点通过定义等价关系 $0 \sim 1$ 进行粘合, 则可得到以下商空间到 $S^1$ 的同胚： $$
[0, 1]/(0 \sim 1) \simeq S^1

$$ 更详细地, 将子空间 $S^1 = \set{ (x, y) \in \R^2 : x^2 + y^2 = 1 }$ 视作嵌入 $S^1 \hookrightarrow \R^2$, 以及以下满的连续映射： $$
\Map{\varphi}{[0, 1]}{S^1}{t}{(\cos(2 \pi t), \sin(2 \pi t))}

$$ 可见 $\varphi(0) = \varphi(1)$, 这个等价关系可以将 $S^1$ 降解为商空间 $[0, 1]/(0 \sim 1)$, 并给出了交换图表 $\vcenter{\xymatrix{
[0, 1] \ar@{->}[r]^{\pi} \ar@{->}[rd]_{\varphi} & [0, 1]/(0 \sim 1) \ar@{->}[d]^{\widehat{\varphi}} \\
& S^1
}}$, 其中 $\widehat{\varphi}$ 是同胚.

证明

首先我们知道 $\widehat{\varphi}$ 显然是个连续函数, 这是因为： $$
\text{$S^1$ 中的开集 $O \in \tau_{S^1}$} \iff \widehat{\varphi}^{-1}(O) \in \tau_\text{Quot} \iff \pi^{-1}\b{\widehat{\varphi}^{-1}(O)} \in \tau_{[0, 1]}

$$ 即是说 $S^1$ 中的任意开集当且仅当是 $[0, 1]$ 中的开集, 由连续函数 $\varphi$ 的定义立即得证.
另一方面, 我们需要确保存在逆连续函数 $\widehat{\varphi}^{-1}$：

可以考虑将 $\varphi$ 限制到开区间 $(0, 1)$ 上, 这显然有逆连续函数 $\varphi|_{(0, 1)}$, 然而由于 $\varphi(0) = \varphi(1)$, 这说明 $[0, 1)$, $(0, 1]$ 皆不是 $[0, 1]$ 中的逆, 唯一的补救方式是将端点商掉, 即 $0 \sim 1$.

例子 4.2.10 (圆柱体, 莫比乌斯带, 环面)

考虑一个正方形, 即 $[0, 1]^2$, 我们可以将它的左右/上下对边分别粘合, 则可构造出环面 $T^2$：

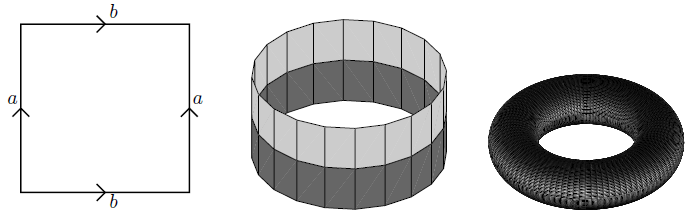
类似地, 如果将左右对边反向粘合, 则可得到以下的莫比乌斯带：

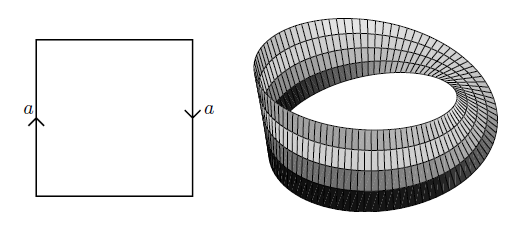
例子 4.2.11 (球极投影)

设 $n \in \N$, 总是存在去除其中一个极点 $N = (0, \cdots, 0, 1) \in S^n$ 的 $S^n$ 与 $\R^n$ 之间的同胚： $$
\R^{n + 1} \supset S^n \backslash \set{N} \overto{\simeq} \R^n

$$ 该映射称之为 球极投影 (stereographic projection).

证明

首先对于 $n = 2$ 的情况, 即是说需要构造映射 $S^2 \backslash \set{N} \to \R^2$, 其中 $S^2$ 的极点为 $N = (0, 0, 1) \in \R^3$, 然后可以将带有原点 $O \in \R^3$ 的二维平面视作 $\R^3$ 下的子空间, 例如： $$
\R^2_\text{P} \coloneqq \Set{ (x, y, z) \in \R^3 : z = 0 } \simeq \R^2 \sub \R^3

$$ 考虑定义一个更广义的映射 $\varphi : S^2 \backslash \set{N} \to \R^2_\text{P}$, 并将球面上的点 $P \in S^2 \backslash \Set{N}$ 映射至投影平面 $\R^2_\text{P}$ 上的一个点 $\varphi(P)$. 从几何上观察, 我们希望构造穿过点 $N, P$, 然后最终抵达 $\varphi(P)$ 的一条直线, 例如以下立体交互图：

现在将 $N, P, \varphi(P)$ 这些直线上的点皆视为向量, 那么我们知道向量 $P - N$ 与该直线保持同一方向 (但从原点 $O$ 出发), 再乘以任意的 $t \in \R$, 那么我们可以获得一条与上述直线平行的长直线 $t(P - N)$, 再将该直线向上 ($Z$ 轴方向) 抬升至 $N$, 记该直线上的一点为 $\ell = (x, y, z)$, 用公式表达即有： $$
N + t(P - N) = \ell

$$ 我们亦可用交互图观察：

可见当 $\ell$ 抬升至 $1$ 时, 它与上方直线重叠, 且将 $\ell$ 限制于 $z = 0$ 时则有 $\ell|_{z = 0} = \varphi(P)$, 可得以下线性方程组： $$
\begin{align}
N + t(P - N) & = \ell \\
\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}
+ t \begin{bmatrix}p_1 \\ p_2 \\ p_3 - 1 \end{bmatrix}
& = \begin{bmatrix}x \\ y \\ 0 \end{bmatrix}
\end{align}
\implies
\begin{dcases}
\begin{aligned}
t p_1 & = x \\
t p_2 & = y \\
1 + t (p_3 - 1) & = 0
\end{aligned}
\end{dcases}

$$ 通过简单的移项, 容易解得 $t = \ds \frac{1}{1 - p_3}$, 因此 $\ds x = \frac{p_1}{1 - p_3}$ 而 $\ds y = \frac{p_2}{1 - p_3}$, 从而建立了映射 $\Map{\varphi}{S^2 \backslash \set{N}}{\R^2_\text{P}}{(p_1, p_2, p_3)}{\b{\frac{p_1}{1 - p_3}, \frac{p_2}{1 - p_3}, 0}}$, 而将该映射推广后则得： $$
\Map{\varphi}{\R^{n + 1} \supset S^n \backslash \set{N}}{\R^n_\text{P}}{(x_1, x_2, \cdots, x_{n + 1})}{\ds \frac{1}{1 - x_{n + 1}} \cdot (x_1, x_2, \cdots, x_n, 0)}

$$ 再由将 $S^n \backslash \set{N}$ 视作为 $S^{n + 1}$ 的子空间以及有理函数是连续的这个结论, 容易得到上述映射是连续的.

另一方面, 利用与上方同样的手段, 需要找出逆映射 $\varphi^{-1} : \R^2_\text{P} \to S^2 \backslash \set{N}$ 并证明它是连续的. 考虑设 $Q \in \R^2_\text{P}$, 我们知道对任意 $t \in \R$ 有： $$
\begin{align}
N + t(Q - N) & = \ell \\
\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}
+ t \begin{bmatrix} q_1 \\ q_2 \\ 0 - 1 \end{bmatrix}
& = \begin{bmatrix} x \\ y \\ z \end{bmatrix}
\end{align}
\implies
\begin{dcases}
\begin{aligned}
t q_1 & = x \\
t q_2 & = y \\
1 - t & = z
\end{aligned}
\end{dcases}

$$ 而将点 $\ell = (x, y, z)$ 限制于 $S^2 \backslash \set{N} = \Set{ (x, y, z) \in \R^3 : x^2 + y^2 + z^2 = 1 } \backslash \set{N}$ 时则有 $\ell|_{S^n \backslash \set{N}} = \varphi^{-1}(Q)$, 那么将上述 $x,y,z$ 分别代入： $$
\begin{align}
(tq_1)^2 + (tq_2)^2 + (1 - t)^2 & = 1 \\
t^2 q_1^2 + t^2 q_2^2 + \b{1 - 2 t + t^2} & = 1 \\
\b{q_1^2 + q_2^2 + 1} t^2 - 2t & = 0
\end{align}

$$ 通过二次通项公式可得两个关于 $t$ 的解分别为： $$
t = 0 \quad \text{或} \quad t = \frac{2}{q_1^2 + q_2^2 + 1}

$$ 再将该结果代入到原来的线性方程组, 容易解得 $(x, y, z) = (0, 0, 1) = N$ 或： $$
(x, y, z) = \b{\frac{2 q_1}{q_1^2 + q_2^2 + 1}, \frac{2 q_2}{q_1^2 + q_2^2 + 1}, \frac{q_1^2 + q_2^2 - 1}{q_1^2 + q_2^2 + 1}}

$$ 从而有 $\Map{\varphi^{-1}}{\R^2_\text{P}}{S^2 \backslash \set{N}}{(q_1, q_2, 0)}{\text{上述结论}}$, 再将该映射推广后则得： $$
\Map{\varphi^{-1}}{\R^n_\text{P}}{S^n \backslash \set{N}}{(x_1, x_2, \cdots, x_n, 0)}{ \frac{1}{x_1^2 + x_2^2 + \cdots + x_n^2 + 1} \cdot \b{ 2 x_1, 2 x_2, \cdots, 2 x_n, x_1^2 + x_2^2 + \cdots + x_n^2 - 1 }}

$$ 同样地, 有理函数是连续的, 这便证得了 $S^n \backslash \set{N} \overto{\simeq} \R^n_\text{P} \overto{\simeq} \R^n$.

命题 4.2.12 (欧氏空间维度的拓扑不变量)

对 $n_1, n_2 \in \N$, 只要 $n_1 \neq n_2$, 则以 $n_1, n_2$ 为维度的欧氏空间, 它们之间不同胚, 即 $\R^{n_1} \not\simeq \R^{n_2}$.

注释

该命题的证明手段不是初等的, 需要用代数拓扑中的上同调等相关工具方可给出证明, 因此证明从略.