点集拓扑 1 - 度量空间, 连续性与紧性
本文内容已完全施工完毕, 读者可放心阅读!
1.0 前言
本笔记以 nLab 上的点集拓扑教程 作参考, 并且将适当地略过一些不重要的证明或例子, 务求尽快建立对拓扑学的认知.
1.1 度量空间
定义 1.1.1 (度量空间)
若 $(X, d)$ 被称为 度量空间 (metric space), 当存在 $X$ 上的 度量 (metric) $d : X \times X \to \R$, 使得对于任意 $x, y, z \in X$ 满足了:
- 正定性 (positive definiteness):$d(x,x) = 0$ 且 $x \neq y \implies d(x, y) \gt 0$;
- 对称性 (symmetry):$d(x, y) = d(y, x)$;
- 三角不等式 (triangle inequality):$d(x,z) \leq d(x,y) + d(y,z)$.
无歧义地通常可将 $(X, d)$ 记为 $X$.
例子 1.1.2 (实数空间 $\R$)
设有实数集 $\R$, 且定义 $\Map{d}{\R \times \R}{\R}{(x,y)}{|x-y|}$, 则能够验证其是度量空间 $(\R, d)$ 的一个度量, 而这个度量空间被称为 实数空间 (real space) 或 直线 (stright line), 并称 $d$ 为 $\R$ 的 通常度量 (usual metric).
定义 1.1.3 (开球 / 闭球 / 球面)
设有度量空间 $X$, 且对于任意 $x \in X$ 以及半径 $\epsilon \in \R^+$ ($\epsilon > 0$), 定义:
- 开球 (open ball):$B^{\circ}_x(\epsilon) := \set{ y \in X : d(x,y) < \epsilon }$;
- 闭球 (closed ball):$B_x(\epsilon) := \set{ y \in X : d(x,y) \leq \epsilon }$;
- 球面 (sphere):$S_x(\epsilon) := \set{ y \in X : d(x,y) = \epsilon }$.
开球 $B^{\circ}_x(\epsilon)$ 亦被称为以 $x$ 为中心, 并以 $\epsilon$ 为半径的 球形邻域 (ball neighbourhood), 或 以 $x$ 为半径的 $\epsilon$-邻域 ($\epsilon$-neighbourhood).
定义 1.1.4 (边界子集)
设有度量空间 $X$, 若子集 $S \sub X$ 被称为 边界子集 (bounded subset) 当 $S$ 被包含于开球 $B_x^{\circ}(r)$ 内, 即 $S \sub B_x^{\circ}(r)$, 其中有 $x \in X, r \in \R$.
命题 1.1.5 (任意点至少存在一个开球, 且都属于它的任意开球)
设有度量空间 $X$ 以及任意点 $x \in X$:
- 存在至少一个开球 $B^{\circ}_x(\epsilon)$;
- 对于任意其余开球 $B^{\circ}_x(\epsilon')$, 有 $x \in B^{\circ}_x(\epsilon') \sub B^{\circ}_x(\epsilon)$.
证明
- 由开球的定义得, 若 $\epsilon > 0$, 则必然能够构造出一个开球, 这是显然的;
- 若设度量为 $d(x, x) = 0$, 则 $x$ 属于它的每一个开球.
命题 1.1.6 (任二开球的交是任意开球的并)
设有度量空间 $X$, 对于任意开球 $B_{x_1}^{\circ}(\epsilon_1), B_{x_2}^{\circ}(\epsilon_2)$, 有: $$
B_{x_1}^{\circ}(\epsilon_1) \cap B_{x_2}^{\circ}(\epsilon_2) = \bigcup_{x \in U} B_x^{\circ}(\epsilon_x)
$$
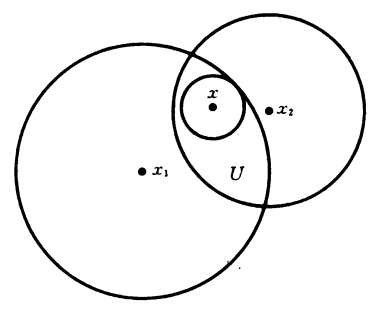
即如图中所示:
证明
设有 $B_{x_1}^{\circ}(\epsilon_1)$ 以及 $B_{x_2}^{\circ}(\epsilon_2)$, 若 $U = B_{x_1}^{\circ}(\epsilon_1) \cap B_{x_2}^{\circ}(\epsilon_2)$, 则透过其定义知 $U \iff (d(x_1,y_1) \lt \epsilon_1) \and (d(x_2,y_2) \lt \epsilon_2)$, 使得对于 $i = 1,2$ 有 $0 \lt \epsilon_i - d(x_i, y_i)$, 那么存在 $x \in U$, 且设 $\epsilon_x = \min(\epsilon_1 - d(x_1,y_1), \epsilon_2 - d(x_2,y_2))$ 则亦可得 $B_x^{\circ}(\epsilon_x) \sube U$, 最终使得: $$
U = \bigcup_{x \in U} B^{\circ}_x(\epsilon_x).
$$
命题 1.1.7 (若点 $y$ 在 $x$ 的任意开球内, 则 $y$ 存在开球包含于 $x$ 的开球中)
设有度量空间 $X$, 以及任意 $x, y \in X$, 且有 $x$ 的开球 $B^{\circ}_{x}(\epsilon)$, 若 $y \in B^{\circ}_x(\epsilon)$, 则存在 $y$ 的开球 $B^{\circ}_y(\epsilon')$ 使得 $B^{\circ}_y(\epsilon') \sub B^{\circ}_x(\epsilon)$.
证明
假设有任意点 $y' \in B^{\circ}_y(\epsilon')$ 以及 $y \in B^{\circ}_x(\epsilon)$, 则需证 $y' \in B^{\circ}_x(\epsilon)$, 即有命题: $$
(d(y, y') < \epsilon') \and (d(x, y) < \epsilon) \implies d(x, y') < \epsilon
$$ 那么将 $d(x, y)$ 与 $d(y, y')$ 相加, 并透过三角不等式则有: $$
d(x, y') \leq d(x,y) + d(y, y') \lt d(x, y) + \epsilon'
$$ 则取 $\epsilon' = \epsilon - d(x, y)$ 使得最终有 $d(x, y') < \epsilon$, 因此 $B^{\circ}_y(\epsilon') \sub B^{\circ}_x(\epsilon)$ 成立.
定义 1.1.8 (赋范线性空间)
设有实线性空间 $V$ 以及 范数 (norm) $\Vert - \Vert : V \to \R_{\geq 0}$, 若 $(V, \Vert - \Vert)$ 被称为 赋范线性空间 (normed vector space), 当对于任意 $v, w \in V$ 满足了:
- 线性性 (linearity):$\Vert cv \Vert = |c| \Vert v \Vert$;
- 三角不等式 (triangle inequality):$\Vert v + w \Vert \leq \Vert v \Vert + \Vert w \Vert$;
- 非退化性 (non-degeneracy):若 $\Vert v \Vert = 0$, 则 $v = 0$.
命题 1.1.9 (赋范线性空间构成度量空间)
任意赋范线性空间 $(V, \Vert - \Vert)$ 若设有度量 $d(x, y) \coloneqq \Vert x - y \Vert$, 则 $(V, \Vert - \Vert)$ 构成度量空间.
例子 1.1.10 (欧氏空间)
对于任意 $n \in \N$, 若有 笛卡尔空间 (Cartesian space) $\R^n = \set{ \vec{x} = (x_i)^n_{i = 1} : x_i \in \R }$, 以及定义 欧几里得范数 (Euclidean norm) 为: $$
\Vert \vec{x} \Vert \coloneqq \sqrt{ \sum_{i = 1}^n (x_i)^2 }
$$ 根据 命题 1.1.9 显然 $(\R^n, \Vert - \Vert)$ 构成度量空间, 被称为 $n$ 维 欧氏空间 (Euclidean space), 无歧义情况下可简记为 $\R^n$.
例子 1.1.11 ($p$-范数)
对于 例子 1.1.10, 我们可以定义一个更广义的例子, 即对于任意 $n \in \N$ 以及 $p \in \R$, $p \geq 1$, 则笛卡尔空间 $\R^n$ 中能定义有 $p$ 范数 ($p$-norm): $$
\Vert \vec{x} \Vert_p \coloneqq \begin{dcases}
\root{p}\of{ \sum_{i} |x_i|^p }, & \quad p \neq \infin \\
\max_{i \in I} |x_i|, & \text{otherwise}
\end{dcases}
$$ 其中若 $p = \infin$ 时称 $\Vert \vec{x} \Vert_{\infin}$ 为 最大范数 (supremum norm), 正如下图所示:

可见当 $p = 2$ 时候就形成了 $\R^2$ 中的单位元, 而 $p$ 趋于无穷时则越来越近似于正方形.
1.2 度量空间中的连续性
定义 1.2.1 (以 $(\epsilon,\delta)$ 定义的连续映射)
对于任意两个度量空间 $(X, d_X)$ 以及 $(Y, d_Y)$, 若函数 $f : X \to Y$ 称为是在点 $x \in X$ 上 连续的 (continuous), 当满足条件: $$
\Forall{\epsilon \in \R \\ \epsilon > 0} \b{ \Exists{\delta \in \R \\ \delta > 0} d_X(x, x') < \delta \implies d_Y(f(x), f(x')) < \epsilon }
$$ 其中对于任意 $x' \in X$. 若 $f$ 被称为是 连续函数 (continuous function) 当其在任意 $x \in X$ 点上都是连续的.
例子 1.2.2 (与子集中任意元素的距离)
设有度量空间 $(X, d)$ 以及 $S \sub X$, 定义函数 $\begin{align} X & \overset{d(S, -)}{\to} \R \\ x & \ \ \mapsto \inf \set{ d(s, x) : s \in S } \end{align}$, 则 $d(S, -)$ 为连续函数, 其中 $\R$ 为欧氏空间.
证明
即需证明, 对于任意点 $x \in X$, 以及任意的 $\epsilon > 0$, 若存在 $\delta > 0$, 且对任意 $y \in X$ 有 $d(x, y) < \delta$ 使得 $|d(S, x) - d(S, y)| < \epsilon$:
由于对任意 $s \in S$ 以及 $y \in X$, 考虑三角不等式: $$
\begin{align}
d(s, x) & \leq d(s, y) + d(y, x) \\
d(s, y) & \leq d(s, x) + d(x, y)
\end{align}
$$ 由于对任意的 $s \in S$, 由于 $d(S, x) = \inf \set{ d(s, x) : s \in S }$ 为 $\set{ d(s, x) : s \in S }$ 的最大下确界, 因此: $$
\begin{align}
d(S, x) & \leq d(S, y) + d(y, x) \\
d(S, y) & \leq d(S, x) + d(x, y)
\end{align}
$$ 使得有 $d(S, x) - d(S, y) \leq d(y, x) \overset{\text{对称性}}{=} d(x, y)$ 以及 $d(S, y) - d(S, x) \leq d(x, y)$, 因此取 $\delta = \epsilon$ 便使得 $|d(S, x) - d(S, y)| \leq d(x, y) < \epsilon$ 成立.
例子 1.2.3 (有理函数是连续的)
- 把实数轴 $\R$ 想象为 $1$ 维的欧氏空间 $\R$, 且对于任意 $P \in \R[X]$ 的实多项式, 则所定义的函数 $\Map{f_P}{\R}{\R}{x}{P(x)}$ 是连续的, 因此多项式为连续函数.
- 平方根函数 $\sqrt{(-)} : \R_{\geq 0} \to \R_{\geq 0}$ 亦是连续的.
定义 1.2.4 (度量空间的邻域与开集)
设有度量空间 $(X, d)$, 则:
- 称 $U_x \sub X$ 为点 $x \in X$ 的 邻域 (neighbourhood) 当存在 $\epsilon > 0$ 使得 $x \in B^{\circ}_x(\epsilon) \sub U_x$.
- 称 $U \sub X$ 为 $X$ 的 开集 (open set) 当对于任意 $x \in U$, 若存在 $\epsilon > 0$ 使得 $x \in B^{\circ}_x(\epsilon) \sub U$.
- 称 $U_x \sub X$ 为点 $x \in X$ 的 开邻域 (open neighbourhood) 当包含了 $x$ 的邻域 $U_x$ 仍是个开集.
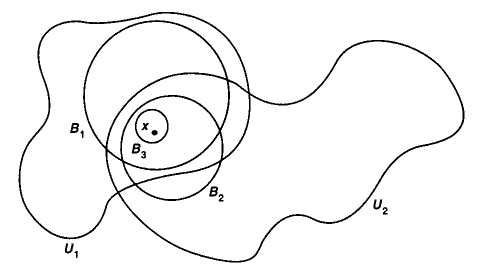
下图便以图像的方式呈现了对于任给的点 $x$, 存在一些开球 $B_i$ 包含了 $x$, 并且有着这些开球所对应的邻域 $U_i$:
例子 1.2.5 ($\R$ 中的开区间构成开集)
设有 $a, b \in \R$:
- 若 $a < b$, 则开区间 $(a, b) = \set{x \in \R : a < x < b}$ 是 $\R$ 中的开集.
- $(a, \infin) = \set{x \in \R, x > a}$, $(-\infin, b) = \set{x \in \R, x < b}$ 以及 $(-\infin, \infin) = \R$ 均为开集.
证明
- 即问对于任意 $x \in (a, b)$, 存在 $\epsilon > 0$ 使得 $B^{\circ}_x(\epsilon) \sub (a, b)$, 那么则仅需限制 $\epsilon = \min(x-a, b-x)$ 即可得证.
- 对于 $x \in (a, \infin)$, 仅需取 $\epsilon = x-a$, 而对于 $x \in (-\infin,b)$ 则取 $\epsilon = b-x$, $(-\infin, \infin)$ 是显然的.
例子 1.2.6 (闭区间, 半开半闭区间, 无穷闭区间均不是开集)
以下这些皆不是 $\R$ 中的开集:
- 闭区间:$[a, b] = \set{x \in \R : a \leq x \leq b}$;
- 半开半闭区间:$(a,b] = \set{ x \in \R : a < x \leq b }$ 以及 $[a, b) = \set{ x \in \R, a \leq x \lt b }$;
- 无穷闭区间:$[a, \infin) = \set{ x \in \R : a \leq x }$ 以及 $(-\infin, b] = \set{ x \in \R : x \leq b }$
定理 1.2.7 (度量空间中开集的基本性质)
设有度量空间 $X$, 则有:
- $X, \empty$ 都是开集;
- 任意多个开集的并仍是开集;
- 有限多个开集的交仍是开集 $\iff$ 任二开集的交仍是开集.
证明
由 命题 1.1.5 (1) 得 $X$ 中的任意点至少都存在一个开球, 显然 $X$ 是开集. 而 $\empty$ 的子集只能是为空, 因此 $\empty$ 亦是开集.
假设有开集族 $\mathcal{U} = \set{ U : \forall u \in U, \exists \epsilon > 0, B^{\circ}_u(\epsilon) \sub U}$ 及它们的并 $\bigcup_{U \in \mathcal{U}} U$, 即证对于任意 $x \in \bigcup_{U \in \mathcal{U}} U$, 存在 $\epsilon > 0$ 使得 $B^{\circ}_x(\epsilon) \sub \bigcup_{U \in \mathcal{U}} U$, 那么现在根据开集族的定义, 则有: $$
y \in \bigcup_{U \in \mathcal{U}} U \iff \exists U \in \mathcal{U}, y \in U \overset{开集族定义}{\iff} \exists U \in \mathcal{U}, y \in B^{\circ}_u(\epsilon) \sub U \quad (\forall u \in U, \exists \epsilon > 0)
$$ 则显然这里有开球 $B^{\circ}_u(\epsilon)$ 包含于 $U$ 且也含于 $\bigcup_{U \in \mathcal{U}} U$ 中, 因此命题成立.假设 $U, V \sub X$ 为开集, 那么它们之间都必然有开球分别含于 $U$ 或 $V$ 中, 且由于 $U \cap V$, 则它们之间存在交点, 而根据 命题 1.1.6, 开球的交是任意开球之间的并, 那么再利用到 $(2)$ 则显然命题成立.
定理 1.2.8 (邻域定义的等价描述)
设有度量空间 $X$, $x \in X$, 则 $X$ 的子集 $U$ 是 $x$ 的一个邻域 $\iff$ $x$ 存在开球包含于 $U$.
证明
$(\Rightarrow)$ 既然 $X$ 的子集 $U$ 是 $x$ 的一个邻域, 根据邻域的定义则 $U$ 中必然含有开集 $V$, 而又根据开集的定义则存在开球 $B^{\circ}_x(\epsilon) \sub V$, 使得有 $B^{\circ}_x(\epsilon) \sub V \sub U$.
$(\Leftarrow)$ 若有 $x \in B^{\circ}_x \sub U$, 那么根据 命题 1.1.7 我们知道开球 $B^{\circ}_x$ 实际上也是个开集使得满足邻域的定义.
定义 1.2.9 (度量空间中的连续映射)
设 $X, Y$ 为度量空间, 映射 $f : X \to Y$ 以及 $x_0 \in X$, 若对于 $f(x_0)$ 的任意开球 $B^{\circ}_{f(x_0)}(\epsilon)$, 存在 $x_0$ 的开球 $B^{\circ}_{x_0}(\delta)$ 使得满足: $$
f(B^{\circ}_{x_0}(\delta)) \sub B^{\circ}_{f(x_0)}(\epsilon)
$$ 则称映射 $f$ 在点 $x_0$ 处是连续的 (continuous at point $x_0$), 并且若任意点 $x \in X$ 都连续, 则称 $f$ 为 连续映射 (continuous maps).
定理 1.2.10 (连续映射的等价定义)
设 $X, Y$ 为度量空间, 映射 $f : X \to Y$ 以及 $x_0 \in X$, 则:
- $f$ 在点 $x_0$ 处是连续的 $\iff$ $f(x_0)$ 的任意邻域的原像是 $x_0$ 的邻域;
- $f$ 是连续的 $\iff$ $Y$ 中任意开集的原像是 $X$ 中的开集.
证明
$(\Rightarrow)$ 需证明:$f$ 在点 $x_0$ 处是连续的 $\implies$ 假设 $f(x_0)$ 的任意邻域 $U$, 根据 定理 1.2.8 有开球 $B^{\circ}_{f(x_0)}(\epsilon) \sub U$, 使得其原像 $f^{-1}(U)$ 应为 $x_0$ 的邻域.
由于 $f$ 在点 $x_0$ 处连续, 所以必定存在 $B^{\circ}_{x_0}(\delta)$ 使得有 $f(B^{\circ}_{x_0}(\delta)) \sub B^{\circ}_{f(x_0)}(\epsilon)$, 而 $B^{\circ}_{f(x_0)}(\epsilon) \sub U$, 因此有: $$
f^{-1}(f(B^{\circ}_{x_0}(\delta))) = B^{\circ}_{x_0}(\delta) \sub f^{-1}(B^{\circ}_{f(x_0)}(\epsilon)) \sub f^{-1}(U) \\
$$ 那么显然地 $f^{-1}(U)$ 包含了开球 $B^{\circ}_{x_0}(\delta)$, 所以就是 $x_0$ 的邻域, 因此命题成立.$(\Leftarrow)$ 需证明:$f$ 在点 $x_0$ 处是连续的 $\implies$ 设 $f(x_0)$ 的任意开球 $B^{\circ}_{f(x_0)}(\epsilon)$, 需找到 $x_0$ 的开球 $B^{\circ}_{x_0}(\delta)$ 使得满足 $f(B^{\circ}_{x_0}(\delta)) \sub B^{\circ}_{f(x_0)}(\epsilon)$.
由于 $f(x_0)$ 的任意邻域 $U$ 的原像 $f^{-1}(U)$ 是 $x_0$ 的邻域, 根据 定理 1.2.8 $x_0$ 就有开球 $B^{\circ}_{x_0}(\delta) \sub f^{-1}(U)$, 则有 $f(B^{\circ}_{x_0}(\delta)) \sub f(f^{-1}(U)) = U$, 取 $U$ 为任意的 $B^{\circ}_{f(x_0)}(\epsilon)$ 则可使 $f(B^{\circ}_{x_0}(\delta)) \sub B^{\circ}_{f(x_0)}(\epsilon)$ 成立.
$(\Rightarrow)$ 需证明:$f$ 是连续的 $\implies$ 设 $Y$ 中任意开集 $U$, 原像 $f^{-1}(U)$ 中以及 $x \in f^{-1}(U)$, 若存在 $\delta > 0$ 使得 $B^{\circ}_{x}(\delta) \sub f^{-1}(U)$, 则 $f^{-1}(U)$ 是 $X$ 中的开集.
若 $f$ 是连续的, 由 $(1)$ 可以得对于任意点 $x \in X$, 都有 $f(x)$ 的任意邻域 $U_{f(x)}$ 的原像 $f^{-1}(U)$ 是 $x$ 的邻域, 那么根据 定理 1.2.8, 那必然存在 $\delta > 0$ 使得 $B^{\circ}_x(\delta) \sub f^{-1}(U)$ 成立.
$(\Leftarrow)$ 需证明:$Y$ 中任意开集的原像是 $X$ 中的开集 $\implies$ 根据 $(1)$, 即对于任意点 $x \in X$, 若有任意邻域 $U_{f(x)}$, 则对任意 $B^{\circ}_{f(x)}(\epsilon) \sub U_{f(x)}$ 进而使得应存在开集 $f^{-1}(B^{\circ}_{f(x)}(\epsilon)) \sub f^{-1}(U_{f(x)})$, 则 $f^{-1}(U_{f(x)})$ 是 $x$ 的邻域.
假设 $Y$ 中任意开集 $B^{\circ}_{f(x)}(\epsilon)$ 的原像 $f^{-1}(B^{\circ}_{f(x)}(\epsilon))$ 为 $X$ 中的开集, 那么由于 $B^{\circ}_{f(x)}(\epsilon) \sub U_{f(x)}$, 所以就有 $f^{-1}(B^{\circ}_{f(x)}(\epsilon)) \sub f^{-1}(U_{f(x)})$ 使得 $f^{-1}(U_{f(x)})$ 为 $x$ 的邻域, 因此命题成立.
1.3 度量空间中的紧性
定义 1.3.1 (序列与子列)
设有集合 $X$, 分别定义:
- $X$ 中元素的 序列 (sequence) 为函数 $x_{(-)} : \N \to X$.
- 子序列 (sub-sequence) 为序列的复合形式, 即 $x_{\iota(-)} : \N \overset{\iota}{\hookrightarrow} \N \overset{x_{(-)}}{\to} X$, 其中 $\iota$ 为单射函数.
定义 1.3.2 (收敛于序列极限)
设有度量空间 $(X, d)$, 若序列 $x_{(-)} : \N \to X$ 被称为 收敛于点 (converge to point) $x_{\infin} \in X$, 记为 $x_i \overset{i \to \infin}{\to} x_{\infin}$, 当满足以下条件: $$
\Forall{\epsilon \in \R \\ \epsilon > 0} \Exists{n \in \N} \Forall{i \in \N \\ i > n} d(x_i, x_\infin) \leq \epsilon
$$ 其中点 $x_{\infin}$ 被称为 $x_{(-)}$ 的 序列极限 (limit of the sequence), 记为 $\lim_{i \to \infin} x_i = x_\infin$.
定义 1.3.3 (柯西序列)
设有度量空间 $(X, d)$, 若 $X$ 中的序列 $x_{(-)} : \N \to X$ 被称为 柯西序列 (Cauchy sequence) 当其满足以下条件: $$
\Forall{\epsilon \in \R \\ \epsilon > 0} \Exists{N \in \N} \Forall{i, j \in \N \\ i, j > N} d(x_i, x_j) \leq \epsilon
$$
定义 1.3.4 (完备度量空间, 巴拿赫空间)
- 若度量空间 $(X, d)$ 中的任意柯西序列都是收敛的, 则称 $X$ 为 完备度量空间 (complete metric space);
- 若赋范线性空间 $(V, \Vert - \Vert)$ 是完备的 (由于赋范线性空间构成度量空间), 则称 $V$ 为 巴拿赫空间 (Banach space).
定义 1.3.5 (列紧度量空间)
若度量空间 $(X, d)$ 被称为是 列紧的 (sequentially compact) 当对于任意 $X$ 序列的子序列都是收敛的.
注释
上述关于列紧度量空间的 $(\epsilon, N)$ 定义可被推广至更一般的拓扑空间中讨论, 因此引出以下的定义与命题.
命题 1.3.6 (列紧度量空间等价于紧度量空间)
设有度量空间 $(X, d)$, 则以下命题是等价的:
- $X$ 是是列紧的;
- 对任意 $X$ 中的开集族 $\set{ U_i \sub X }_{i \in I}$ 覆盖了 $X$, 若存在有限子集 $J \sub I$ 仍覆盖了 $X$.
注释
- 任意开集族 $\set{ U_i \sub X }_{i \in I}$ 被称为 覆盖 (cover) 了 $X$, 若满足 $X = \bigcup_{i \in I} U_i$;
- 若在更广义的拓扑空间中讨论, 则开集族 $\set{U_i \sub X}_{i \in I}$ 被称为覆盖了 $X$ 的 开覆盖 (open cover).
- 这里不详细描写证明过程, 因为更方便的证明方式将于后续的章节铺垫完基础工具后再作介绍.